Fancy Lunar Landers

Posted on Edited on

There was a very interesting lab in the course of Unsupervised Learning, Recommenders, Reinforcement Learning taught by Prof. Andrew Ng, which trains a machine learning model to make sure the lunar lander land in a pre-defined range of area. In the course, Andrew also mentioned one of his team's great work that using machine learning model to drive a toy helicopter flying inverted in the real word. That's amazing, the work they have done has been published: Autonomous Helicopter Aerobatics through Apprenticeship Learning.

The entire lab is based on the Gymnasium, which provides experiential environments for reinforcement learning. After finished the lab, I noticed the Gymnasium is quite flexible and easy to extend, making it possible to play the env in some fancy ways beyond the default configuration.

1. Lunar Lander Hover

To make the LunarLander hover in the air instead of landing, basically we'll need to redefine the reward model.

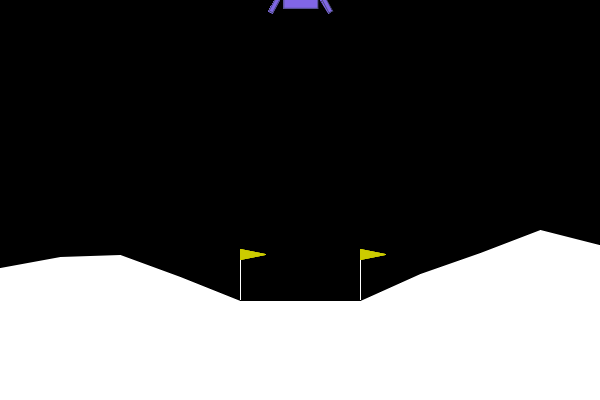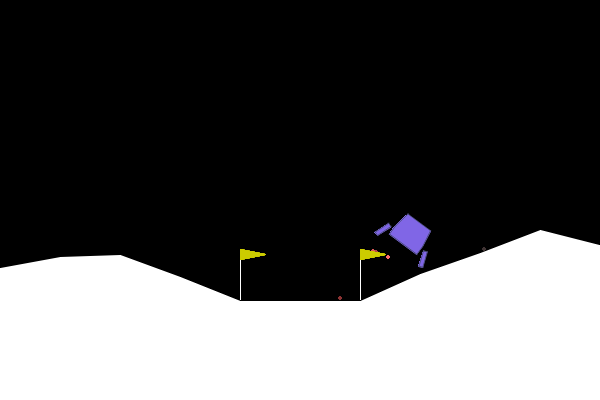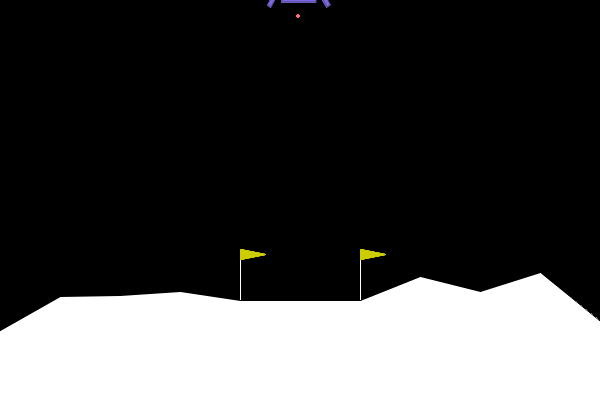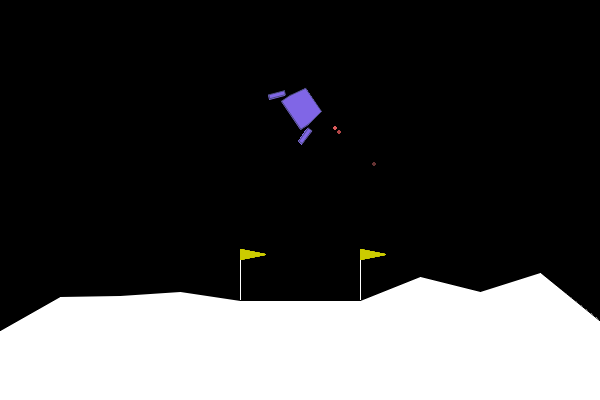
According to the original LunarLander, the target is to land on the ground with 2 legs, and the landing position should be between the two flags:

Per the documentation of LunarLander-V3, the reward model is:

1
2
3
4
5
6
7
8
9
10
11
For each step, the reward:

is increased/decreased the closer/further the lander is to the landing pad.
is increased/decreased the slower/faster the lander is moving.
is decreased the more the lander is tilted (angle not horizontal).
is increased by 10 points for each leg that is in contact with the ground.
is decreased by 0.03 points each frame a side engine is firing.
is decreased by 0.3 points each frame the main engine is firing.

The episode receive an additional reward of -100 or +100 points for crashing or landing safely respectively.
An episode is considered a solution if it scores at least 200 points.

Comparing the landing reward, seems hover can be way more easier, since we only need to limit the position vertically and horizontally, no need to concern of fuel and landing posture.

Extend the original LunarLander

To adjust the original LunarLander reaching our new target: hover, the reward model needs to be updated. And benefit by the open sourced code of gymnasium, we can directly extend the LunarLander by overriding a few methods.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class FancyLunarLander(LunarLander):
    def __init__(self, x_range, y_range, **kwargs):
        super().__init__(**kwargs)
        self.max_step_reward = 1.0
        self.max_angle_error = 1.0
        self.safe_x_range = x_range

        self.target_y = 1.0
        self.max_height_error = y_range

    def update_range(self, x_range, y_range):
        self.safe_x_range = x_range
        self.max_height_error = y_range
    
    def step(self, action):
        obs, reward, terminated, truncated, info = super().step(action)
        x, y = obs[:2]
        
        # horizontal
        if abs(x) <= self.safe_x_range:
            zone_reward = 0.2 * (1 - abs(x) / self.safe_x_range)
        else:
            zone_reward = -2.0 * (abs(x) - self.safe_x_range)

        # vertical
        height_err = abs(y - self.target_y)
        if height_err < self.max_height_error:
            height_reward = 0.5 * (1 - height_err / self.max_height_error)
        else:
            height_reward = -1.0 * (height_err - self.max_height_error)

        # composed rewards
        reward = zone_reward + height_reward

        return obs, reward, terminated, truncated, info

In the override method step() , we at first call the super method to get necessary outputs such as the observations, terminated, truncated and information, which are no need to change at all and will be returned by our override method.

The only change introduced is the "reward", because in our "FancyLunarLander" we don't want to follow the original reward model, which is designed to land in a limited area. Our new goal is to hover, so what we need is letting the LunarLander stick in a 2D area, which we can define the vertical and horizontal positions.

According to the override method, obviously, we limit the 2D area to a square that coordinates are x = [-x_range, x_range], y = [1 - y_range, 1 + y_range]. The less the x_range / y_range are, the smaller the square is.

Besides, the reward model needs to be redesigned, which as per the code, if the current position of the LunarLander is in the square, it increases the reward by adding positive values (zone_reward and height_reward) to the reward variable, on the contrary, if the current position is out of the square, the reward will be decreased due to negative values to be added.

Let's see an example of the model outputs:

Looks it works very well!

2. Lunar Lander Inverted Hover

The previous chapter proves it's relatively easy to stay a hover status if appropriate rewards are provided. So can we have an inverted hover like the paper did if we set appropriate rewards as well?

Unfortunately, the answer is no, inverted hovering wouldn't be that easy to build like a plain hover. Two obstacles are preventing us from achieving that:

  1. Standard lunar lander can only produce positive thrust.

    To make lunar lander hovering, all we need to do is adjusting the main power to produce positive thrust combining with fine adjustments of left/right engines. But it's impossible for having positive thrust only if the lunar lander is in the inverted status, since positive thrust would just accelerate the lunar lander to crash.

  2. Inverted position is not a common and easily achievable posture

    In Gymnasium, the initial status of lunar lander, is in upright position with random velocity/angular velocity, it's difficult & inefficient to set several rewards toward inverted hover state and letting reenforcement learning model to discover the correct movements by itself.

To overcome the above 2 obstacles, first we need change the lunar lander source code to have negative thrust, then we are going to use the approaches from the paper, which is “Apprenticeship Learning for Target Trajectory”, to learn from expert trajectory.

Negative thrust

In Gymnasium, there are two envs of lunar lander, discrete or continuous. At this time we are going to use the continuous env which allows us passing Box(-1, +1, (2,), dtype=np.float32) as the action for more precise control. For the lunar lander, the main engine will be turned off completely if main < 0 and the throttle scales affinely from 50% to 100% for 0 <= main <= 1

What we need to modify is to unlock the limitation of no power if main < 0. Instead, we would want the main engine outputs negative thrust when main < 0.

The version of Gymnasium we are using is v1.2.3, locate to the code we can find the limitation of main power at here:

1
2
3
4
5
f self.continuous:
    m_power = (np.clip(action[0], 0.0, 1.0) + 1.0) * 0.5  # 0.5..1.0
    assert m_power >= 0.5 and m_power <= 1.0
else:
    m_power = 1.0

As we'll use the "continuous" mode so we only need to change the clip and assert to the following:

1
m_power = (np.clip(action[0], -1.0, 1.0))

With the minor change, we create a class named BidirectionalLunarLander, extends from LunarLander and override the entire step() method containing the change as well. (Full code see here)

Now we have negative thrust, let's move on to the next step.

Apprenticeship Learning for Target Trajectory

Considering the difficulty of pushing the RL model to randomly learn a way to flip, it's better to positively find a way that probably drives the lunar lander flip to inverted posture. Once it goes into inverted, then we try to make it stable in the position.

Based on the BidirectionalLunarLander, with several attempts, I created a naive_inverted_controller that can produce actions to make the lunar lander flip in most cases. It has nothing to do with "learning", it also isn't an optimal controller, it's just a "naive" controller:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def navie_inverted_controller(obs, phase, sign):
    x = obs[0]
    y = obs[1]
    vx = obs[2]
    vy = obs[3]
    theta = obs[4]
    omega = obs[5]

    # angle wrap to [-pi, pi]
    theta_wrapped = np.arctan2(np.sin(theta), np.cos(theta))
    theta_abs = abs(theta_wrapped)

    side = 0
    main = 0
    if phase == 1:
        if y > 1.4:
            return np.array([0, 0], dtype=np.float32), phase
            
        if theta_abs < 1.9:
            side = -0.6 * sign
            main = 0.8
        elif theta_abs > 1.9 and abs(omega) > 0.1 :
            side = 1 * sign
            main = -1
        else:
            phase = 2

    if phase == 2:
        if y > 1.4:
            return np.array([0, 0], dtype=np.float32), phase

        main = -0.6
        if vx > 0.1:
            side = 0.5
        elif vx < -0.1:
            side = -0.5
        else:
            side = 0

    return np.array([
        np.clip(main, -1.0, 1.0),
        np.clip(side, -1.0, 1.0)
    ], dtype=np.float32), phase

Many hard coded statics are in the implementation, but don't worry, it works on our BidirectionalLunarLander and can be used to generate training data later.

Once we can confidently drive the lunar lander to flip, next is how to make it stable in the inverted position without crash. Obviously our naive controller is only good at flip, it cannot fine control the lunar lander towards stabilization. But with the experience of the previous chapter - lunar lander hover - it's straightforward to stable the lunar lander by using reenforcement learning.

First we build a Env wrapper that overrides the default reward model to the reward model dedicated for inverted hovering:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class InvertedHoverWrapper(gym.Wrapper):
    def __init__(self, env, controller, y_ref=1.2):
        super().__init__(env)
        self.controller = controller
        self.y_ref = y_ref

    def reset(self, **kwargs):
        obs, info = self.env.reset(**kwargs)
        self.controller.reset(obs[2])

        for _ in range(200):
            action, phase = self.controller.act(obs)
            obs, _, terminated, truncated, _ = self.env.step(action)

            if terminated or truncated:
                obs, info = self.env.reset(**kwargs)
                self.controller.reset(obs[2])

            if phase == 2:
                break

        return obs, info

    def step(self, action):
        obs, _, terminated, truncated, info = self.env.step(action)

        reward = self.tracking_reward(obs, action)

        done = terminated or truncated
        if abs(obs[1]) > 3.0:
            done = True

        return obs, reward, done, False, info

    def tracking_reward(self, obs, action):
        x, y, vx, vy, theta, omega, _, _ = obs
        main, side = action
    
        theta_err = np.arctan2(
            np.sin(theta - np.pi),
            np.cos(theta - np.pi)
        )
    
        reward = (
            - 4.0 * theta_err**2
            - 2.0 * omega**2
    
            - 3.0 * (y - self.y_ref)**2
            - 2.0 * vy**2
    
            - 3.0 * x**2
            - 2.0 * vx**2
    
            - 0.1 * main**2
            - 0.05 * side**2
        )
    
        return reward

The controller being passed to __init__ is exactly our naive controller, and we use the naive controller to operate the lunar lander to inverted position when reset() is called. Hence, while training the model by using the wrapper, the initial position is considered as inverted already, the RL model only needs to keep the position as long as possible.

This time as we are using the continuous control model, DQN might not be a good choice. SAC will be better.

Using SAC along with the InvertedHoverWrapper, we could train a good RL model that is able to stay the lunar lander in inverted position. Combined with naive controller, we can build a HybridExpert to operate the BidirectionalLunarLander:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class HybridExpert:
    def __init__(self, inverted_controller, rf_policy):
        self.inverted_controller = inverted_controller
        self.rf_policy = rf_policy
        self.phase = 0

    def reset(self, vx0):
        self.inverted_controller.reset(vx0)
        self.phase = 0

    def act(self, obs):
        if self.phase != 2:
            action, phase = self.inverted_controller.act(obs)
            self.phase = phase
            return action
        else:
            action, _ = self.rf_policy.predict(obs, deterministic=True)
            return action

Let's see how the HybridExpert works:

Expert Distillation

Now we already have the HybridExpert that is capable of flipping the lunar lander to inverted and keep it stable. But there are some flaws of the HybridExpert:

The flipping movement is made by a classic controller instead of a machine learning model. There's a phase stored in the object determine whether to act by the naive controller or by the RL model. The controlling is discontinuity in separate stages, making the HybridExpert lacks of generalizability.

To have a universal, generalized model capable of output actions from the beginning of the env reset to the end state, we should perform a sort of thing that training another model learning from the HybridExpert, that is expert distillation.

We are going to use the combination of Behavior Cloning and DAgger to train a new model from HybridExpert.

Behavior Cloning

This is quite straightforward, we have the HybridExpert in our hand, we let it run thousands of times, record all trajectories as the training data, use the data to train a neural network.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def build_bc_policy(obs_dim=8, act_dim=2):
    inputs = layers.Input(shape=(obs_dim,))
    x = layers.Dense(128, activation="relu")(inputs)
    x = layers.Dense(128, activation="relu")(x)
    outputs = layers.Dense(act_dim, activation="tanh")(x)

    model = models.Model(inputs, outputs)
    return model

# record HybridExpert movements(observations and actions) into 'data'
obs_all = data["obs"]          # (N, 8)
actions_all = data["actions"]  # (N, 2)
dataset = tf.data.Dataset.from_tensor_slices(
    (obs_all.astype(np.float32), actions_all.astype(np.float32))
)

dataset = dataset.shuffle(10000).batch(256).prefetch(tf.data.AUTOTUNE)
policy = build_bc_policy()
policy.compile(
    optimizer=tf.keras.optimizers.Adam(learning_rate=3e-4),
    loss="mse"
)
policy.fit(
    dataset,
    epochs=30
)

The neural network is a very simple model who has two hidden layers that contain 128 parameters for each, input = 8 and output = 2.

But this is like learning drive by watching drive videos, even we have record thousands of "videos" that HybridExpert has well operated, but it doesn't know how to do if in the position it's never seen.

Hence, sometimes the model will crash the lunar lander:

DAgger

By using the DAgger approach, we let our neural network model (the learner) to output actions from the input observation, but let the HybridExpert (the expert) to act based on the same observation. Appending the expert output actions into the dataset, so that the dataset now contains more abundant trajectories.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def dagger_rollout(
    env,
    policy,
    expert,
    max_steps=500
):
    obs, _ = env.reset()
    expert.reset(obs[2])

    rollout_data = []

    for t in range(max_steps):
        # learner action
        obs_batch = obs.reshape(1, -1).astype(np.float32)
        learner_action = policy(obs_batch, training=False).numpy()[0]

        # expert label
        expert_action = expert.act(obs)

        rollout_data.append({
            "obs": obs.copy(),
            "action": expert_action.copy()
        })

        obs, _, terminated, truncated, _ = env.step(learner_action)

        if terminated or truncated:
            break

    return rollout_data

Using dagger_rollout to get more data and append to the dataset, train it again, then we'll get our final model. Let's see what it got now:

Ref

Full Code